Jednym z problemów regulacji ciągłej jest dobór nastaw regulatorów wchodzących w skład układu automatycznej regulacji. Regulator może mieć strukturę P, PI lub PID. W literaturze możemy się spotkać z algorytmami doboru nastaw regulatorów według Zieglera-Nicholsa. Są to metody opracowane doświadczalne, prezentujące poszczególnych nastawy regulatora:
-wzmocnienia kp,
-czasu całkowania Ti,
-czasu różniczkowania Td.
Wartości poszczególnych nastaw ustalono na podstawie zdejmowanych charakterystyk funkcji przejścia obiektu. Podczas wielu eksperymentów powstały dwie podstawowe metody Zieglera-Nicholsa, które następnie były rozwijane i modyfikowane.
Pierwsza metoda Zieglera-Nicholsa
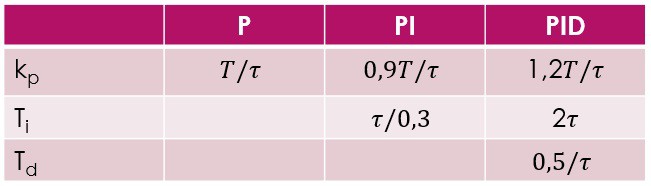
W celu wyznaczenia nastaw regulatora należy eksperymentalnie zdjąć odpowiedź rzeczywistego obiektu na pobudzenie skokiem jednostkowym. Jeśli obiekt nie zawiera elementu całkującego, ani dominujących biegunów zespolonych, wówczas odpowiedź na skok jednostkowy ma kształt litery S. Tego typu krzywą aproksymujemy do postaci opisanej transmitancja: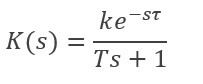 
Ziegler i Nichols zaproponowali w tym przypadku dobór parametrów w UAR z regulatorem P, PI, PID według zależności przedstawionych w tabeli:
Druga metoda Zieglera-Nicholsa
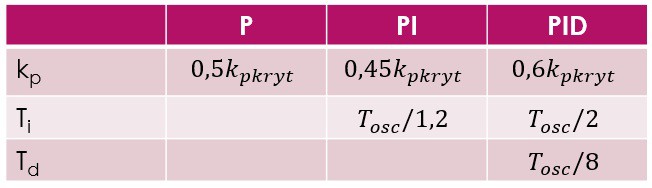
Druga metoda Zieglera-Nicholsa została opracowana już w latach 40-stych. Wykorzystuje się w niej informacje dotyczące obiektu wyznaczane podczas specjalnego badania go w układzie zamkniętym z użyciem prostego regulatora typu P. Wykorzystując drugą metodę Zieglera-Nicholsa zakłada się, że transmitancja obiektu KO(s) nie jest znana. Procedura doboru nastaw poszczególnych regulatorów polega na wyłączeniu w układzie zamkniętym działania całkującego i różniczkującego oraz stopniowym zwiększaniu współczynnika wzmocnienia do wartości, przy której w układzie powstają oscylacje niegasnące tzn. o stałej amplitudzie (układ znajduje się na granicy stabilności). Wzmocnienie to nazywa się wzmocnieniem krytycznym kpkryt. Drugim parametrem jest okres powstałych oscylacji niegasnących Tosc, który można odczytać na podstawie wykresu sygnału wyjściowego powstałego dla kp=kpkryt. Wyznaczanie powyższych parametrów pokazano na rysunku.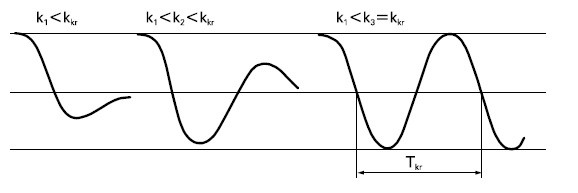 
Nastawy regulatora przedstawiono w tabeli:
Zaprezentowana metoda jest powszechnie cytowana, a jej szczególne modyfikacje implementowane są w algorytmach automatycznego doboru nastaw. Jednak należy zwrócić szczególną uwagę na fakt, iż podczas badań należy doprowadzić układ do granicy stabilności. W procesach przemysłowych wszelkie odchylenie od punktu pracy wiąże się ze stratami energii i surowców, a co najmniej pogorszeniem jakości produktu, dlatego tak drastyczne odchylenia, w niektórych przypadkach nawet groźne dla instalacji produkcyjnej, mogą być niedopuszczalne. Nie ma też określonych miar jakości procesu uzyskiwanych z tak dobranymi nastawami. Należy się liczyć z tym, że w konkretnym przypadku jakość nie będzie zadowalająca. Metodę należy zatem traktować jako skuteczną dla przypadku typowych obiektów i użyteczną dla ustalenia bazy wyjściowej do poprawy nastaw podczas dalszego użytkowania układu regulacji. Z tych powodów wydają się nie mieć znaczenia nieznaczne różnice wartości liczbowych współczynników w powyższych wzorach, jakie spotyka się w opracowaniach różnych autorów.
Należy również zauważyć, że w przypadku, gdy model matematyczny obiektu jest znany ( znana jest jego transmitacja KO(s)), możemy zastosować metode rozmieszczania pierwiastków w celu znalezienia wartości wzmocnienia krytycznego kpkryt oraz pulsacji oscylacji niegasnących wkryt.